Orbit of the Moon before the Flood
This analysis begins by specifying the initial conditions for the Earth and the Moon before the flood. It is assumed that about 3% of the Earth’s mass was expelled by the fountains of the great deep during the flood, and 1.22% of that mass impacted the Moon.8 As explained on pages 359– 364, the great majority of that expelled mass became TNOs. Therefore, the flood slightly altered the mass of the Earth and Moon. The gravitational parameter, µ, is equal to the gravitational constant, G, times the mass of an object. Subscripts indicate if the parameters are for the Earth (E) or Moon (M) and to designate whether a quantity is before the flood (BF) or after the flood (AF).
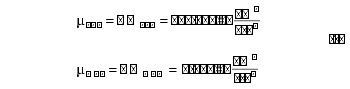
For small masses, like man-made satellites that orbit the Earth, it is common to ignore the mass of the satellite when calculating orbital parameters, because their mass is so much smaller than the Earth. However, for large bodies, like the Moon, calculations need to account for the mass of the orbiting body. Therefore, the combined gravitational parameter of the Earth and Moon will be used for the analysis here.
It is also assumed that the Moon’s orbit was a perfect circle before the flood, so its eccentricity was zero, and it had a semimajor axis of 395,884 km.
Finally, there were also 360 days in a year before the flood, not today’s 365.242 days per year. [See Endnote 35 on page 193.]
Given these initial conditions, the velocity of the Moon’s circular orbit and its period before the flood were,
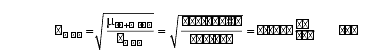
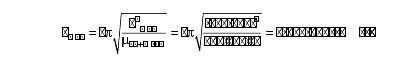
To convert this period into days, this number must be divided by 86,400, which is the number of seconds in one day. Also, to account for the longer length of a day before the flood, it also needs to be multiplied by the ratio of 360/365.242.
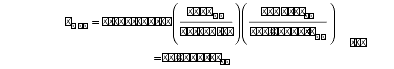
This is called the sidereal period. It is the time required for the Moon to travel 360° around the Earth and arrive at the same point relative to the stars. However, because the Earth moves relative to the Sun, the Moon has to revolve more than 360° around the Earth between successive full Moons (the definition of a synodic period, or lunar month). If there were exactly 12 lunar cycles in a year before the flood, the Earth would have moved 30° each month around the Sun
. As a result, the Moon would have had to revolve an extra 30° around the Earth for each lunar cycle. This is illustrated in Figure 13
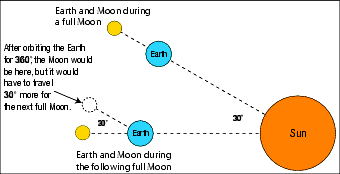
Figure 13: Synodic Period, the Time from Full Moon to Full Moon. Before the flood, a lunar month (or moonth) was 30 days, so the Moon had to revolve around the Earth 30 ° more than one complete revolution—or 390° total.
Therefore, before the flood, the Moon would have had to revolve 390° around the Earth to make one complete lunar cycle, and the synodic period (SP) would have been
which is what people on the Earth would have used to determine the length of a month before the flood.