The Debris When It Arrived at the Moon
It is assumed the debris’ orbit can be treated as a two-body problem as it traveled to the Moon, meaning the debris was only affected by the Earth’s gravity until it reached the Moon’s sphere of influence. Therefore, the specific energy and eccentricity did not change.
Using the value for eD found in Equation 10, the velocity of the debris was calculated when it arrived at the Moon’s distance from the Earth (395,884 km from Equation 3). Notice, Equation 15 is the same as Equation 10; it is just rewritten here to solve for velocity now that energy is known. Also, the subscript “DM” denotes the debris’ position, R, and velocity, V, when it arrived at the Moon.
This is the magnitude of the velocity vector, but its components are needed to determine how the debris affected the Moon’s orbit. To find these components, the true anomaly and flight path angle must be calculated first.
True anomaly, n, is the angle from perigee to the position vector. This is found using the solution to the two-body equation of motion given in Equation 16.
Rewriting this to solve for true anomaly,
It is now easy to estimate the time it would have taken for the debris to travel to the Moon. The debris was in a slightly hyperbolic orbit (e = 1.000004), and it arrived at the Moon’s sphere of influence with n = 179.388°. The travel time can be accurately estimated as the time required to travel to apogee (n = 180°) in an elliptical orbit (e slightly less than 1.0). This can be found by calculating half of the period for an elliptical orbit with a semimajor axis that was half the distance between the Earth and Moon before the flood, or 197,942 km. Using these values, it would have taken five days for the debris to reach the Moon’s sphere of influence, and very shortly after that it would have impacted the Moon.
The flight path angle, g, when the debris arrived at the Moon’s sphere of influence is found next. This is the angle of the velocity vector above the local horizon as shown in Figure 14. The horizontal component of the velocity vector is 
, and the vertical, or radial, component of the velocity vector is
.
can be found by taking the derivative of the solution to the two-body equation of motion, given in Equation 16. Only true anomaly, n, changes. The parameter, p, and eccentricity, e, would not change. Therefore,
Referencing Figure 14, the flight path angle can be calculated using Equations 16 and 19.
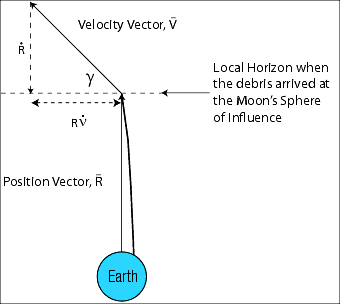
Figure 14: Flight Path Angle, g, of the Debris When It arrived at the Moon. This figure is drawn looking down at the North Pole.
This equation allows the flight path angle to be calculated for the debris when it arrived at the Moon. As found in Equation 14, the eccentricity of the debris’ orbit was barely greater than 1.0, and from Equation 17, the true anomaly of the debris when it reached the Moon’s distance from the Earth was 179.388°. Therefore,
Using this value and the magnitude of the velocity vector, found in Equation 15, the two components of the debris’ velocity are found when it was 395,884 km from the Earth (the distance between the Earth and Moon before the flood). Because these calculations assumed the debris was in an equatorial orbit, the horizontal direction was eastward, and there would have been no component of the velocity vector in the northern or southern direction.
